ESCHER
TRASFORMACIÓN DE MÓDULOS BASADA EN UNA RED DE POLÍGONOS.
TRASLACION:
El plano puede ser llenado mediante una red de polígonos regulares: cuadrados, triángulos, rombos o hexágonos.
A partir de estos polígonos, mediante unas sencillas transformaciones, podemos obtener nuevas figuras equivalentes (con la misma superficie) que también llenarán el plano.
Las transformaciones que podemos realizar son:
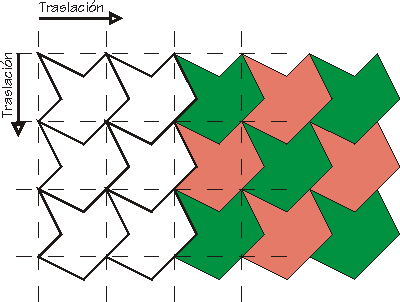
Con este sistema podemos conseguir nuevas figuras que llenen el plano a partir de cualquier paralelogramo.
En este ejemplo trabajaremos
con un cuadrado.
con un cuadrado.
El proceso es sencillo, sólo tenemos que cortar un trozo del cuadrado adyacente a un lado y trasladarlo al lado opuesto
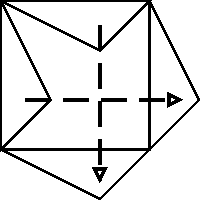

Este proceso lo podemos repetir las veces que queramos, la figura que obtenemos siempre tiene la misma superficie que el cuadrado original y encajara consigo misma siempre que cada nueva pieza siga un movimiento de traslación respecto a la original. como se muestra ahora.
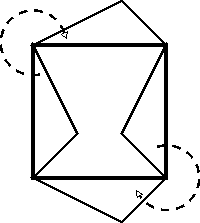
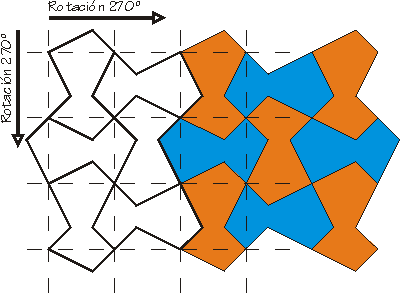
 ROTACION SOBRE UN EJE:
Con este sistema también podemos conseguir nuevas figuras que llenen el plano a partir de cualquier red de polígonos que lo hagan y tengan dos lados contiguos iguales.
En este ejemplo trabajaremos con un cuadrado.
El proceso es sencillo, sólo tenemos que cortar un trozo del cuadrado adyacente a un lado y rotarlo al lado contiguo usando el vértice común como centro de giro.
| |||||||
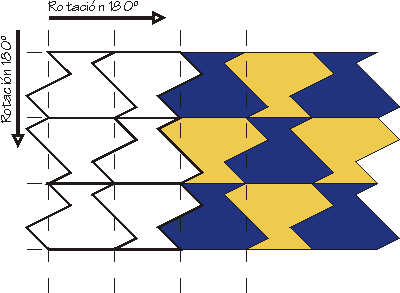
ROTACION SOBRE EL MISMO EJE:
Con este sistema también podemos conseguir nuevas figuras que llenen el plano a partir de cualquier red de polígonos que lo hagan.
Trabajaremos con un cuadrado como en los dos anteriores:
El proceso es sencillo, sólo tenemos que cortar un trozo del cuadrado adyacente a la mitad de un lado y rotarlo sobre el mismo lado usando el punto medio como centro de giro.
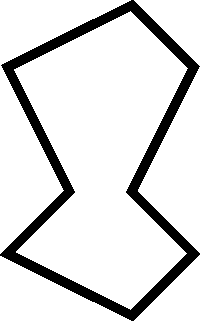
Yo realice un ejemplo y esto fue lo que resulto:
esta marcada la cuadricula.
y como propuesta hice fue una decoración interna, con mosaico como lo hice en el ejemplo anterior... | |||||||





No hay comentarios.:
Publicar un comentario